Kada izgubimo telefon, novčanik ili ključeve, uglavnom koristimo nekoliko trikova da ih pronađemo. Vraćamo se istim putem na mesta na kojima smo bili. Ili tražimo na svim mestima gde obično ostavljamo ove predmete. Možda pokušavamo da se setimo svih neobičnih mesta na kojima smo bili u poslednje vreme. Svaki od ovih načina je logičan.
Kada entitet koji raspolaže ogromnim resursima izgubi nešto izuzetno vredno, kao što je na primer nuklearna podmornica, onda se u pomoć pozivaju topovi Bajesovske teorije (po engleskom matematičaru Tomasu Bajesu) pretraživanja upomoć.
Na sreću za nas obične smrtnike, osnovni koncept ove teorije je dovoljno jednostavan da nam može pomoći u pronalaženju predmeta u svakodnevnom životu. Čak i ako predmet koji nedostaje vredi samo stotinak dinara, ovaj matematički proces može pojednostaviti logiku naše pretrage, štedeći nam vreme i novac.
Čoveče, gde mi je auto?
Verovatnoća da se izgubljeni predmet nađe na jednom mestu u odnosu na drugo je intuitivan koncept koji se može pretvoriti u matematički objekat. Jednostavna mapa, podeljena u mrežu, sa svakom sekcijom koja ima dodeljenu verovatnoću da sadrži određenu stavku, je oblik funkcije gustine verovatnoće.

Napravite mapu verovatnoće
Recimo da ste automobil ostavili na parkingu sa 100 mesta, a sada ste zaboravili gde ste parkirali. Najosnovnija funkcija gustine verovatnoće parkiranja prikazuje jednu kutiju za svaki prostor, svaki sa verovatnoćom od 1/100 (ili 0,01).
Pretpostavimo dalje da niste invalid, a postoji deset mesta za osobe sa invaliditetom. Sada funkcija gustine verovatnoće više izgleda kao 0,011 na 90 mesta i 0,001 u svakom zabranjenom mestu. (I dalje se ostavlja 10% šanse da ste pogrešili i nepropisno se parkirali).
Sada unosimo još neke podatke. Deset parking mesta najudaljenijih od prodavnice je prazno. Šanse da vaš auto bude tamo su nula. Sada vaša funkcija gustine izgleda kao 80 kvadrata sa verovatnoćom od ~0,0125. Ako obično kružite oko parkinga kako biste pronašli mesto za parkiranje najbliže ulaznim vratima prodavnice, onda će na tim mestima biti veća verovatnoća, a na udaljenijim manja.
Poenta je da svaki put kada dodate još neku informaciju, funkcija gustine verovatnoće se menja. Dakle, na ovaj način možete da suzite i ubrzate pretragu, počevši od mesta koja imaju naveću verovatnoću da ste tu parkirali automobil, i nastaviti niz listu, proveravajući mesta sa najnižom verovatnoćom kao poslednje rešenje.
Da li je pas pojeo moj domaći?
Prva tehnika je dobra, ali druga je još bolja. Ova druga mapa sadrži, za svaku oblast pretrage, šansu da se na njoj zaista nalazi predmet koji tražimo.

Verovatnoća da nađemo svesku ako je pas pojeo je nula
Na primer, ne možemo da naćemo svesku sa urađenim domaćim zadatkom. Ako je domaći zadatak na praznom stolu, sigurno biste je odmah videli. Ako ste je ostavili na pretrpanom stolu, prekrivenom gomilama papira, šanse su vam manje. Da li je mogla da odleti kroz prozor zbog promaje? Znači da postoji šansa da je u dvorištu. Ako je pas pojeo svesku, šansa da je nađete je nula.
Sada, uzmite ove dve karte raspodele verovatnoće i pomnožite ih zajedno. Bilo koja oblast za pretragu u kojoj postoji mogućnost da se sveska nalazi i ima veliku verovatnoću da ćete je pronaći ako je tamo, biće predstavljena relativno velikim brojem. Ovo su dobra mesta za početak vaše pretrage. Oblasti u kojima je predmet lako uočiti, ali je malo verovatno da će tamo biti, ili će ga verovatno biti teško uočiti, imaju manji broj. Ovo su niži prioritet pretrage. Oblasti u kojima to nije verovatno i gde ga ne možete lako uočiti – kao na primer da je pojeo pas – potiskuju se na poslednje mesto.
Pronalaženje begunca
Dok pretražujete oblasti sa najvećom kombinovanom verovatnoćom, trebalo bi da ponovo procenite svoje pretpostavke i da ažurirate svoju mapu verovatnoće kako napredujete.
Recimo, tražite odbeglog osuđenika. Vaš čopor pasa za praćenje može namirisati gde je nedavno bio. U blizini zatvora je put koji vodi do autobuske stanice. Verovatnoća da će potrčati tim putem kako bi uhvatio autobus je relativno velika, a velike su i vaše šanse da ga uočite ako je blizu otvorenog puta (za razliku od, recimo, šume). Stajalište sa staklenim zidovima gde se autobusi pojavljuju samo sporadično ima slično visoku kombinovanu verovatnoću.
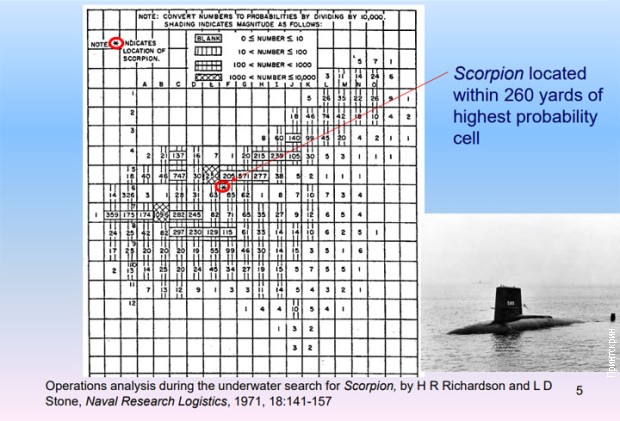
Primena Bajesovske pretrage u potrazi za nestalom podmornicom 1971. godine
Ako pretražujete put, a psi ne osete nikakav miris, onda je verovatnoća da se on nalazi na nekoj lokaciji dalje od puta znatno smanjena. Autobusko stajalište je takođe lokacija manje verovatnoće. S druge strane, ako psi nešto nanjuše, verovatnoća autobuske stanice se povećava.
Ako sve ovo zvuči relativno jednostavno, to je zato što jeste. Trik metode je da koristite inteligentno rezonovanje u vašim distribucijama verovatnoće, uključujući i način na koji ih modifikujete dok tražite.
Funkcija gustine verovatnoće gde bi se objekat mogao nalaziti posebno zahteva ozbiljno razmišljanje. Najbolji način da se formira takva funkcija nije nagađanje ili pretpostavka nasumične slučajnosti, već razvijanje niza hipoteza o tome zašto je nestala i mapiranje gde će se najverovatnije nalaziti. U oblasti pretrage dodelite verovatnoću svakom kvadratu za svaku hipotezu, a zatim pomnožite te verovatnoće zajedno.
Bajesova pretraga je zdrav razum + matematika
U slučaju nestalog broda, nekoliko polja verovatnoće bi se moglo konstruisati počevši od hipoteze i prateći njene verovatne zaključke. Prva hipoteza bi mogla biti da je najverovatnija lokacija centar blizu mesta gde je ostvaren poslednji radio kontakt, a verovatnoća se smanjuje što se dalje udaljavate od te lokacije.
Druga hipoteza bi mogla biti da ako je uragan prošao kroz to područje, putanja oboda oluje je najverovatnije mesto na kome je došlo do potonuća broda. Ako se nađe komad krhotina broda kako pluta u jednoj oblasti, onda se verovatnoća da se brodolom dogodio u blizini povećava, a verovatnoća da je daleko opada.
Ako postoji jaka struja koja teče kroz oblast sa krhotinama, onda uzvodna putanja te struje dobija veću verovatnoću, proteže se nazad onoliko koliko je tekla od kada je brod izgubljen. Područja nizvodno imaju opadajući niz verovatnoće.
Bajesova pretraga je destilacija zdravog razuma, formalizovana i unapređena sa relativno jednostavnim matematičkim konceptima. Ako tražite izgubljeno blago od milijardu dolara, sigurno ćete sesti za računar da mapirate distribuciju verovatnoće i matematički ih kombinujete.
Ako ste u jednosatnoj potrazi za svojim novčanikom, brza i jednostavna mentalna primena Bajesovske metode pretrage može vam uštedeti vreme i povećati šanse za uspeh.
































